2015年,四川省实行了二三本合并。今年,专科批次的专一、专二合并成了一个批次。批次合并必然造成以往的批次线划定位次发生变化,因此,运用批线差来定位学校就会出现偏差,在这种变化的情况下,如何较好的实现分数定位学校呢?这里给大家介绍一种我们近年来提出的新方法——高位分差法。
二本、三本合并,一本扩容后,如何根据分数定位学校是摆在高三学生及家长面前极为迫切而严峻的问题,因为相当多原来的二本院校挤入一本来招生,一本分数线相比于以前变化比较大,各学校的录取分及平均分相对于一本线将出现变化,如果再用原来的分差进行定位时,就会出现误差。再者,二本、三本合并后,原来的二本线、三本线相比于现在的二本线都会有一定的变化,因此用原来的三本分差或者二本分差都会出现问题。具体变化情况如图所示:
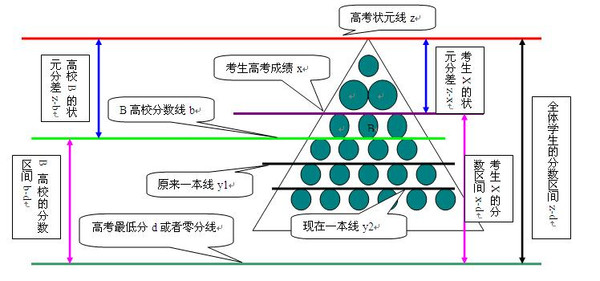
上图中,中分段到高分段的学校分布如三角形中的圆,原一本线y1为根据扩容前高校及招生计划划定的省控分数线,现一本线y2为部分二本高校及招生计划加入一本行列后划定的省控线。这样,高校B的分差就由原来的b-y1 变成了b-y2,显然二者并不相等。因此,我们再无法用原来的分差b-y1来进行定位。
在此情况下,我们就不能仅将眼睛盯在分数线的划定比例上,而应当放弃用省控线计算分差的方法,把目光用来寻找变化中的不变。通过观察可以发现,无论高校加入多少,一本分数线划定存在高与低,但高校录取线的相对位置是不变的,因为高校录取分数线距离高考状元的相对位置不变。
为解释这个相对位置,这里引入了状元分差的概念,引入这一概念的基本假设是:每年考生的成绩分布呈比较标准的正态分布,这样就可以用学校距离状元分数的远近来描述其相对位置。因为高考状元的分数高低带有一定的偶然性,这就会导致高位分差仍有一定的偏差。于是,我们就取相对比较稳定的较高位次,比如,对于四川省的学生来讲,理科的高位分数取全省第60名的成绩,文科的高位分数取全省第30名的成绩。当然学校的分数中有三个指标,录取分、平均分、专业分,可以分别用三个指标与高位分相减,但一般建议大家用学校平均分这一指标,也就是学校平均分高位分差,一般就用g-bp来表示。
明白了学校高位分差的计算后,再来计算学生自己的高位分差,也就是用今年的高位分数减去学生自己的高考成绩(用g-x)。这样实际上就是计算学生距离高位分有多远,学校距离高位分有多远,如果学生与高位分之间的分数距离小于学校与高位分之间的分数距离,那么就意味着学生的分数高于学校的分数,也就是说,学生有很大可能被学校录取。即如果学生的高位分差(g-x)<(g-b),那么学生就可以被B高校录取。
但上式中说的都是今年的指标,但今年的这个b(也就是高校的录取分数)是无法知道的,这时一般就用往年的这个指标了,前一年的这个指标用g1-b1来表示,前两年的这个指标就用g2-b2来表示,前三年的指标用g3-b3来表示。如果我们自己计算的(g-x)小于(g1-bp1)、(g2-bp2)、(g3-bp3)中的任何一个,就可以说有最大的把握进入这个学校。因为我们实际上有极大概率高于这个学校的平均分了,也就是说学生的排名比学校靠前,就可以被相应的学校录取。
